Contango and Backwardation are sets of terms that refer to two different things; I attempt to define, explore and compare the industry terms with their respective meanings in academics and futures theory.
Part I: Industry Definition (Contango and Backwardation)
Futures are contracts that guarantee the delivery of a certain commodity at a predetermined time, usually at monthly delivery intervals. Therefore if the market expects the spot (the market value for immediate settlement) of a certain commodity to be higher at time A than time B, the futures contract that delivers during time A will trade at a higher price than time B. This mechanic gives us an easy way to gauge the market expectations of spot price at any time in the future.
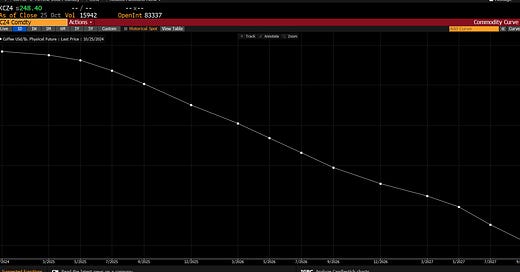
Keep in mind that futures contracts range in price as the time until expiry (the date of delivery) varies. The chart that describes this is called the forward curve, which details a future contract’s price x months or years from today. Therefore, as the spot price (current market price) is 0 months from today, the spot price will always be the value of the curve at t=0. It is important to keep in mind that forward curves provide a glimpse of contract pricing at a single point in time; the actual forward curve can change as time and market conditions change. Here’s an example of a forward curve for a coffee future:
Notice that as time until expiry increases, the contract’s price decreases; this phenomenon is known in industry terms as backwardation, the downward sloping forward curve. The inverse of this phenomenon is called contango, in which the price of the contract at an expiry further in the future is more than the price of contract with an earlier expiry. Contango and backwardation are commonly used when comparing some forward price to the current spot price, though any two points (with each point representing the price of a future x months from now) can create the curve; the first point does not necessarily need to represent current spot.
Part II: Academic and Theoretical Definition (Normal Contango and Normal Backwardation)
This is, in my opinion, the more interesting of the two sets of definitions. Let’s make clear that contango and normal contango are not the same thing; the industry term, contango, was defined in part one of this article, while normal contango is confusingly different concept. The same goes for backwardation and normal backwardation.
Before defining normal contango and normal backwardation, let’s review some terms that will be used in the definitions:
Contract Price is the market price for a certain future. Remember, a future is a contract that guarantees the delivery of a certain of a commodity at a certain time. (an example of a future could be a contract that delivers 100 troy ounces of gold three months from now)
Expiry is the date of delivery for the contract.
Expected Spot is the market’s expectation for what the spot price (the market price for immediate settlement, or the price of the good if you want it now) will be at expiry. Please keep in mind that expected spot, though it exists, is impossible to derive or know for certain. Much of a future contract’s value consists of the market expectation of the spot price at expiry, but not all of it. The expected spot’s elusiveness is much like Benjamin Graham’s intrinsic value concept.
With that out of the way, let’s now move to definitions and theory.
When futures reach settlement, the price of the contract will always equal equal the underlying commodity’s spot price; this makes sense, as both spot and future contracts now guarantee immediate delivery of the same commodity. However, the direction the contract’s price takes there is not as simple; there are two ways the futures contract price can merge with spot price: normal contango and normal backwardation.
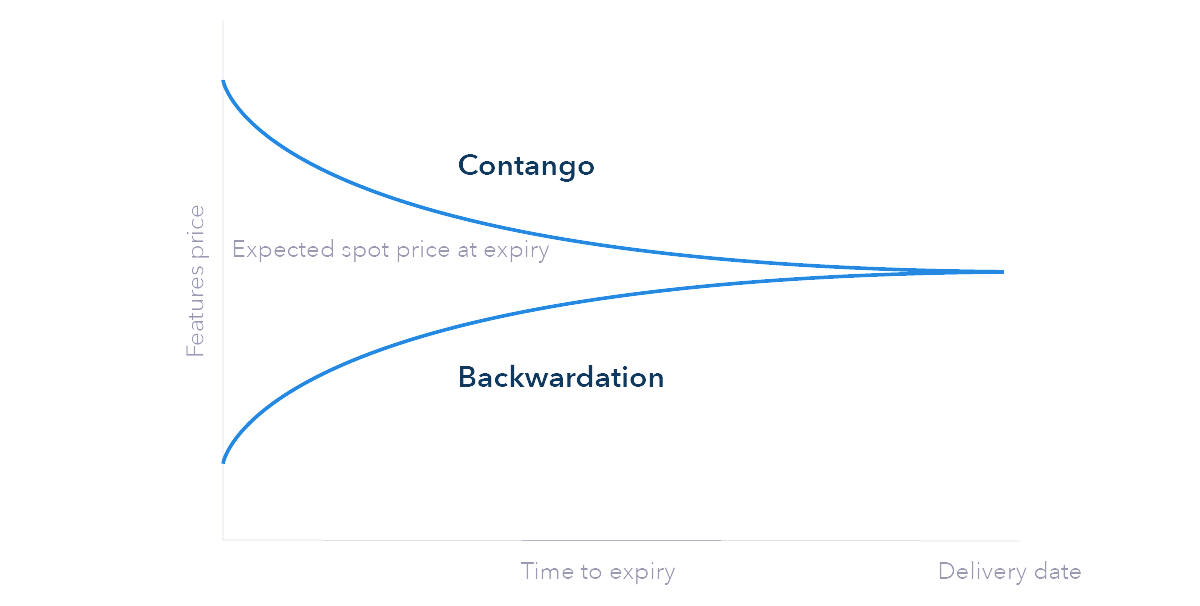
Normal contango (in which the contract price approaches expected spot by descension) more commonly reflects the movement of futures contract pricing. As commodities cost capital to store, an individual who seeks to have a commodity at some time in the future would rather hold a contract rather than the commodity itself, even though they result in the same outcome (having a given amount of the commodity a given time in the future). The futures market knows this and, through supply and demand, finds a premium for the futures, the carrying cost, which is the gap between expected spot price on delivery and futures contract price. This premium diminishes over time as the next best alternative, storing the actual commodity until delivery, naturally lessens in price as well. (it costs more to store a barrel of oil for two years than one year)
Normal backwardation, on the other hand, makes less sense; why would the market allow one to pay lower for a futures contract than the expected price of the goods delivered at expiry? I have chewed on this question for a week or so and have come up with only two answers; negative carrying costs and spot hedging.
Negative carrying costs are, in fact, quite an intuitive reason for the ascending nature of the normal backwardation curve; if diminishing carrying costs result in the descension and eventual merger of the normal contango curve with expected spot, diminishing negative carrying costs should naturally result in an ascending normal backwardation curve. But how can negative carrying costs be possible? You never get paid to hold something… except when you do!
For example, holding a house includes the negative carrying cost of charging rent, and holding stock in a company includes the negative carrying cost of dividends. As the time to collect negative carrying costs diminishes as time until expiry decreases, the gap between expected spot and future price diminishes, compressing the gap (aka the negative carrying costs) between the normal backwardation curve and expected spot.
Yet as the time to collect inflow diminishes, wouldn’t the value of the position diminish with it? It would, but keep in mind the the future contract is the alternative to this position, not the position itself; just as the positive gap between the contango curve and expected spot diminishes over time as the negative opportunity cost of buying the future (evading carrying costs) diminishes as well, the backwardation curve has a negative premium (in other words a discount), implying that the alternative way of having a given amount of the commodity at a certain time in the future (aka holding the commodity) will include negative carrying costs, which will diminish as time progresses.
The second reason for normal backwardation comes from the nature of a futures contract. Let’s imagine you are a mining company that knows a certain amount of copper will be extracted from its mines in the next fiscal year. As a supplier, it doesn’t make sense to sell all the copper mined at spot price; the market for copper can cause the price to go up (which would be favourable), but can also cause the price to drop (which would be detrimental). Therefore, if you wanted to guarantee some revenue or gain some liquidity, you could sell futures that expired after you had harvested or mined your product. In this case, by pre-selling some copper at a certain price, you hedge spot exposure (the price fluctuations of the commodity don’t affect you anymore, as you have already sold your good at a set price through the futures contract).
Now would companies want to hedge spot exposure more in volatile markets or calmer, more predictable markets? The more volatile markets provide less certainty, so suppliers seeking to hedge would want to sell more futures for commodities with volatile spot prices. At a larger scale, this selling could contribute to the contract price lowering; there might even be a case in which sellers are willing to sell futures at a price below the expected spot, paying the premium of selling at a lower price in exchange for spot hedging. What we just described is, again, the backwardation curve! The gap between the backwardation curve and expected spot therefore could be, in addition to negative carrying cost, the premium sellers pay for spot hedging.
I hope some of the above thoughts and definitions provided interesting food for thought; I’ll continue to think for more explanations for the normal backwardation curve. Understanding both sets of contango and backwardation is important for both commodities traders and individuals looking for arbitrage opportunities in futures markets.




This is a specific and informative article. The ideas are very clear and evidently well thought out. It helped me gain more understanding about futures and the stock market.